Now Trigo in Form 4 got 3 things to know:
1. unit circle and corresponding angle (IMPORTANT! and hardest to learn)
2. Special angles. (not in SPM, basically is shit unless school teacher decide to kena them)
3. Graphs of sin tan cos
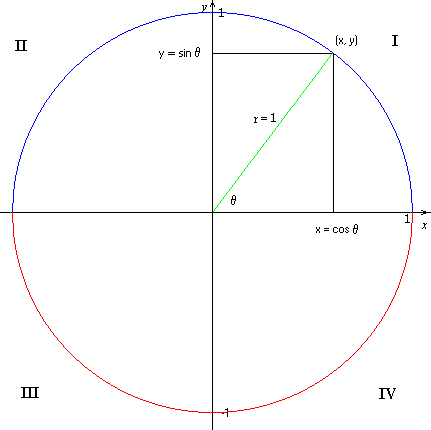
1. it is cut into 4 parts, each part called a "quadrant".
2. the quadrant starts from top right, called quadrant I, then go anti clockwise, quadrant II, III and IV.
3. The radius for this circle is 1 UNIT. So if you draw any right angle triangle that TOUCHES the circumference, you can see that the hypotenuse is FOREVER 1. (Important theory to know if you are working with sin and cos)
4. How to measure angle? Basically the angle is measured from the X-AXIS of FIRST QUADRANT
Example:
a. If you look at the all the circles, all the GREEN colour angles are the ORIGINAL angle formed by the red line and x-axis. (ignore the black line that forms the triangle for now)
If you can see, these angles all start from the x-axis from 1st quadrant and turn until they reach the red line.
b. the BLUE colour angle that you see, is what we call CORRESPONDING angle. As you can see, corresponding angles are LESS than 90 degree, and measured STARTING from the x-axis on its own quadrant. (For first quadrant, ori angle = cor. angle)
c. So original angle in
Quadrant I = 0.000000000001 to 90
Quadrant II = 90.0000000000001 to 180
Quadrant III = 180.000000000001 to 270
Quadrant IV = 270.0000000000001 to 360 or 270.00000000000001 to 0
d. Relationship between cor and ori angle
In Quadrant I, ori = cor
Quadrant II, as you can see, ori + cor = 180.
Quadrant III, 180 + cor = ori
Quadrant IV, ori + cor = 360.
(Different book give different rules, actually is just 搬来搬去 only, like quadrant II they give 180 - ori = cor)
5. If you form a triangle on each quadrant (Now look at the black lines), As you know, we can find cos sin tan on every right angle triangle using adjacent, opposite and hypotenuse lines. Because original angle is more than 90 degrees, we only find the cos sin tan for corresponding angle.
SOHCAHTOA
cos = adj/hyp sin = opp/hyp tan = opp/adj
Notice that in any of your quadrants, adjacent line falls on x-axis, and opposite line falls on y-axis.
Ok, so now we are finding VALUES of cos sin tan in EVERY quadrant.
In quadrant I, both x-axis and y-axis are positive, and hypotenuse is positive everywhere (Pythagoras Theorem, even if 'a' or 'b' is negative, after square is positive, so 'c' is positive)
So cos is +x/1 = + value. ('x' because adj falls on + x-axis line, so we use +x)
sin is +y/1 = + value
tan = +x/+y = +
So in first quadrant, ALL positive
Repeat for every quadrant, you will get:
Quadrant II: cos tan -, sin +
Quadrant III: cos sin -, tan +
Quadrant IV: sin tan -, cos +
If you summarize from Quadrant I to IV, it is ALL, SIN, TAN, COS positive
So use this to make them rmb: All Scientist Talk Crap, OR All Science Teacher Crazy (Not Science Tutor ar! Later Science Dpt have war with us liao LOL)
So this is the first thing that we can get from unit circle. Second thing is, how to find the trigonometric value of an angle, given the coordinates?
Refer to the first diagram again.
Rmb just now we say adj = x, opp = y. So now adj = 0.6 units, opp = 0.8 units.
So we can use any of cos sin tan to find teta (I will put teta as O for now)
tan O = opp/adj
tan O = 0.8/0.6
tan O = 1.33333333
O = 'shift' tan 1.33333 (use calculator, IMPOSSIBLE to use your brain)
O = 53.13 degrees
Very easy right? Now lets use harder examples.
1. Determine coordinates, quadrant, and in that quadrant, sin cos tan which is positive.
2. Work out solutions
1. Coordinates of Q are (-0.5, -0.87). In Quadrant III, tan is positive, sin cos are negative.
2. sin O is opp/hyp, = y/1
sin O = -0.87 = D
Now, can you find WHAT is ANGLE O?
sin O = -0.87
If you follow the workings in the previous example. You will not get your answer.
O = 'shift' sin -0.87
O = - 60.46???? (NEGATIVE?) negative actually means turn in the terbalik way, means instead from quadrant I x-axis turn anticlockwise, we turn clockwise 60.46 degree. That will bring us into Quadrant IV, but the answer isn't correct either, we should be in Quadrant III. HOW!!!????
So this is the limit of calculator. Because sin O = -0.87 GOT TWO ANSWERS. one falls in Quadrant III, one in Quadrant IV. (All Scientist Talk Crap, sin is negative in Quadrant III and IV). Calculator can only show one answer. So students always panic, cannot get answer.
So now the trick is, use CORRESPONDING ANGLE APPROACH.
So now, take away the negative sign. Let sin O = 0.87. In these questions, tell students that negative or positive is just INDICATOR to tell you whr the quadrant is.
sin O = 0.87
O = 'shift' sin 0.87 = 60.46
Now you know that the corresponding angle is 60.46, how to convert to original angle?
In Quadrant III, ori angle = 180 + corresponding angle
Therefore, The angle that we want is 180 + 60.46 = 240.46.
So we found the answer, dont need to use the 'negative' sign at all. So must tell them, when press calculator, DONT input NEGATIVE, or else confuse themselves only. (of course if you are pro, know the theory super superbly well, can work de, but I myself oso tend to get confuse so I dont recommend input negative)
So typical exam question is like this de:
In these questions, things to do:
1. Put all the info given in place
2. Determine whether to use ori angle or corresponding angle. (99.9% use corresponding de la, whr got test ori so easy de?)
3. Determine the relationship between ori and corr angle, and find the quadrant
4. Find out in the quadrant, sin cos tan which is positive and negative
5. Work out solutions.
1. cos x = 3/5, means adj/hyp is 6/10. Hence AC is 10cm, and BC will be 8cm.
2. We need to find y. y is greater than 90 degree. So we use corresponding angle to help us to find original angle.
3. Whr is corresponding angle???? you can see that y is outside the triangle. The angle ACB (next to y) should be corr angle. Means corr + y = 180. 180 degree is in which quadrant? In quadrant II lo. (90 to 180, dun take 180 to 270)
4. In Quadrant II, sin positive, tan cos negative
5. We are finding TAN y. Tan y = - tan (angle ACB) <------- see the negative? Cause' in quadrant II, corresponding tan is negative.
tan (angle ACB) = opp/adj
tan (angle ACB) = 6/8
tan (angle ACB) = 3/4
tan y = - tan (angle ACB)
tan y = - 3/4 = C
So you can try to find angle y also. ;)
Answer: 143.13 degree
YAY NOW WE FINISH 1st part. Still got special angles and graph OMGWTFBBQMCB.
Special angles actually is derived from 2 types of triangles.
To see how to derive, see http://sk19math.blogspot.com/2007/05/special-angles-in-trigonometry.html
You can combine the sin cos tan to see a clearer picture. I will upload last year notes for your info. the notes oso got how to derive but very simple version, and got give you a list of the angles
Part III, graph. See the notes la LOL
1. In their syllabus, only 0 to 360 degree. they only need to know sin x, cos x, and tan x graph. If they ask got -sin x ar, sin -x etc etc ar, tell them NO, that is in Add Maths, and say "i think u are in wrong class u can go AM class now" lol
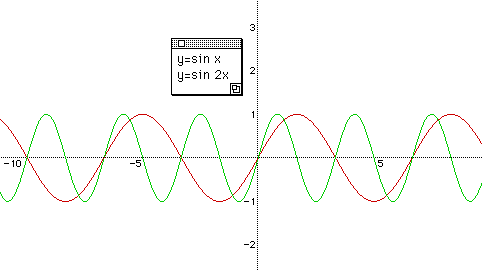
***** But 2005 they got ask sin 2x. But i dunno why, cause' shouldn't ask de. If sin 2x, the graph basically becomes
If sinx = 1, x is 90
If sin 2x = 1, x is 45 lo. (Sin 2(45) = 1), so at your x-axis, sin 2(180) = sin 360, and sin 2(360) = sin 720. Means if you have sin2x graph, you basically draw sin x graph twice. You pick few points then try to plot la then I think u understand de.
2. Their careless mistake: Example,
Most of them will choose A. Because they just look at the shape of the graph then put. So dikenakan dy. They din check the x-axis. x-axis is until 180 only. Because for A, the x-axis should be until 360 degree. So 180 degree should be half part of the graph only. Answer is C
Thats all you need to know for Trigo. Walao A...I think my longest post ever.
Thats all la. Signing off noobiak. Paiseh 2nd part 3rd part very rush cause going out for wedding dinner jor.
